🥇 Fibonacci series

The Fibonacci series, the Phi number and how they manage to describe the universal proportions, which are part of the world around us

Leonardo de Pisa was an Italian mathematician, who has been better known throughout the world as Fibonacci. This mathematician discovered a sequence commonly known as “The Fibonacci series”; he came up with this idea when calculating the number of rabbits that could be obtained over the period of several months, after inducing them to breed.

Suppose that at the beginning of the first month we have a pair of newborn rabbits. Therefore, we have one (1) pair of rabbits that will take a month to develop enough to be able to pair. So at the end of the first month, we can already cross this pair of rabbits, and we will have 1 + 0 = 1 couples, the same pair of rabbits, because they have not yet procreated.

Now, at the end of the second month the first couple gives birth to a second pair of rabbits, and the first pair pairs again, but (of course) they have not yet sired them and in this case we will already have 1 + 1 = 2, to a couple of pairs rabbits.

By the end of the third month, the first pair of rabbits gives birth to a third pair, while the second pair is turning one month old, and they come together to pair, only that the first pair crosses again. In this case, the first pair already had two pairs of rabbits. Therefore, the number of rabbit pairs for this month will be: 2 + 1 = 3

If we follow the succession, at the end of the fourth month, the first pair of rabbits will have already produced three pairs of rabbits, while the second pair will already have had their first pair of rabbits. We would then have that the number of rabbit pairs would be: 3 + 2 = 5.

If we continue doing these calculations, we would have that, if we start with the numbers 1 and 1 + 0 = 1 and add them both, it would give us the number 2 as a result, so that:

• 1 + 1 = 2

• 1 + 2 = 3

• 2 + 3 = 5

If we continue adding the last result with the previous one, we can obtain the rest of the series. So we can continue building the sequence, always with the sum of the two previous results:

• 5 + 3 = 8

• 8 + 5 = 13

• 13 + 8 = 21 and so on

Fibonacci sequence

How this sequence influences the explanation of certain proportions in nature

This type of mathematical pattern is found in countless examples within nature. For example, the number of petals a flower has almost always matches a number in the Fibonacci series. While it is true that some flowers have 3 petals, you will find others that have 5 petals, while some will have 8 and you can even find flowers with up to 13 petals. But in very few exceptions, you will find a flower with a number of petals that does not match a Fibonacci number. That is, with 4, 6, 7, 9, 10 or 11 petals.

The numbers that belong to this series are presented in a big part of the world that surround us.

In the year 1753 a Scottish mathematician named Robert Simson discovered that the quotient of two consecutive numbers in the Fibonacci series always tends to be closer to 1.6180339. The result will always be alternatively, a number somewhat above and later, another a little below 1.6180339, but yes, without reaching it absolutely.

The number to which the relationship between two successive numbers of this same series converges, was called the golden number, which in addition to being irrational, is denoted by the Greek letter Phi.

If you notice how the seeds that are in the center of any sunflower are arranged, you will notice that each seed is at a certain angle with respect to the previous one, which corresponds to approximately 137.5º.

You can obtain this same angle by multiplying the decimals of the Phi number by 360º, and you will obtain an angle greater than 180º. If we take the complement of this angle, it will give us as a result 137.5º which coincides with what we call the golden angle.

This allows the seeds to have the optimal filling, that is, the same space between one seed and another. Resulting in a distribution of seeds from the center to the periphery and completely covering the area, in the most suitable way possible. This is how the new leaves that are generated in the sunflower do not block the sun from the previous leaves and also cover the maximum of the surface, thus managing to receive as much rain as possible. This same phenomenon occurs with the leaves of an artichoke.

But, this does not end there, if you count the spirals that form in the center of a sunflower, you will realize that there are 89 spirals in one direction and 55 in the other; they can also have 144 and 89, where again these three numbers belong to the illustrious succession.

Trees do not escape this analogy, since if you look closely at the angle that is formed between two consecutive branches, you will realize that they have an angle of approximately 137.5º between them.

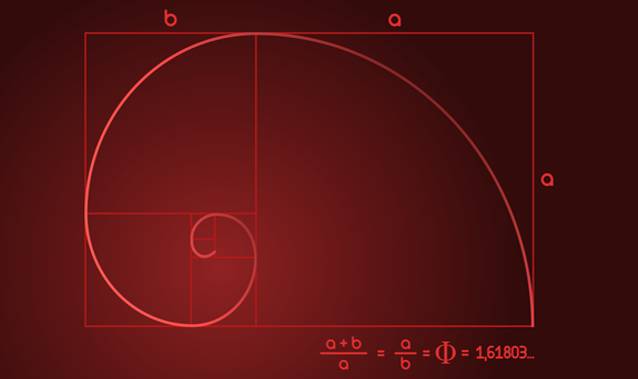
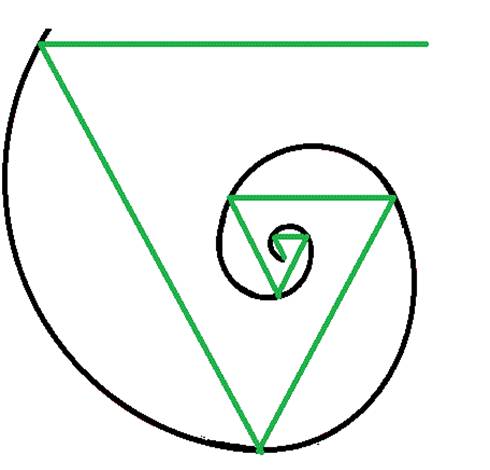
The succession created by Leonardo de Pisa is also related to the so-called golden spiral, which is generated by drawing a series of adjacent squares, the sides of which are made up of the terms of the Fibonacci series. The spiral is formed by the arcs of circumference, which are formed by the radii of the sides of these squares.

cephalopod mollusk

If we look at the shell of the nautilus (cephalopod mollusk) we can see the similarity with the golden spiral, only that instead of forming the spiral with the sides of a square, it is formed with equilateral triangles. Both spirals differ in the opening, but in both cases they have the same length to generate the first polygon.

Shell Spiral Drawing

Not satisfied with the similarities described in advance, we can also note that equivalent spirals are present in certain galaxies and hurricanes.

Galaxia final Hurricane

The Fibonacci series and the golden ratio in art

Great music composers in the 20th century, such as Olivier Messiaen, Delia Derbyshire, Béla Bartók, and the band Tool, used this famous succession to invent new structures for their musical chords.

This Phi number has been directly involved in art for thousands of years. Since it also interferes with the ideal proportions of certain ancient architectural structures.

This is because again the Phi number is also obtained when we divide a line into two certain unequal parts. If we take the quotient of the longest part and the smallest part, it will end up being equal to the total length of the line divided by its longest part. That is to say:

a / b = (a + b) / a

Where “a” is the longest part of the line and “b”, the shortest. We can see that the Pyramid of Giza has a length of 230 meters on each side of its base and its height is 146 meters. The relationship between the two measures is approximately 1.575, which, as we can see, is quite close to the golden number.

Those numbers can be applied to the proportions of a rectangle, called the golden rectangle, considered one of the most visually satisfying geometric shapes.

Even the famous mathematician and sculptor Phidias, born in 500 BC, is believed to have applied the Phi number to the design of the sculptures in the Parthenon.

On the other hand, a Franciscan friar named Luca Bartolomeo de Pacioli was an economist, accountant, mathematician and highly recognized for being one of the forerunners of probability calculus. This friar published a book on mathematics in 1509 called “De divina proportione”, which was illustrated by none other than Leonardo da Vinci. There he claimed that “Without mathematics there is no art” and this compendium of writings, only intended to reveal the secret to the artists about harmonic forms, using the golden ratio as the main tool.

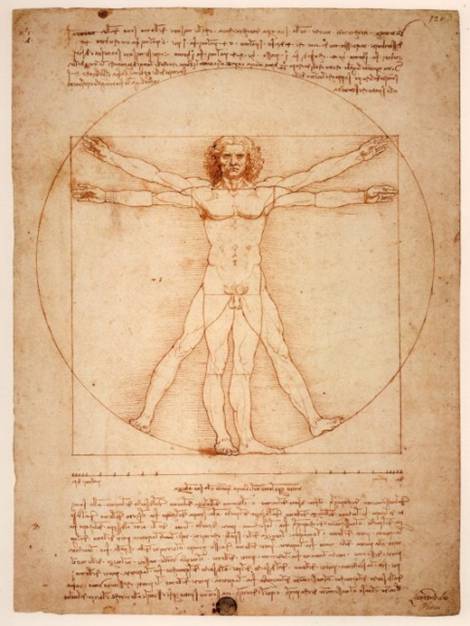
In fact, Leonardo da Vinci himself, through what he called the “sectio aurea”, defined the ideal symmetry in his paintings such as “The Mona Lisa”, “The Last Supper” and “The Vitruvian Man”.

Leonardo Da Vinci

Da Vinci claimed that the ideal proportion of a person is closely linked to the quotient between the measurement of his height and the distance from the ground to his navel, since for a harmonious human being this relationship tended to Phi. In the same way, this number was repeated in an approximate way with the relationship between the distance between his fingers to his shoulder and the measurement from the elbow to his fingers. In fact, “The Vitruvian Man” was designed with these proportions.

As if that weren’t enough, this sequence has multiple applications in mathematics, computer science, and even game theory. A mathematical curiosity is to add ten consecutive numbers chosen at random from the famous series; You will notice that the result of the sum will always be a multiple of 11. As we can see, that the Fibonacci series is full of mathematical anecdotes, which can fascinate anyone who delights in this type of event.